| 硬い芯材 | Jul.22,2002 |
革は引っ張りや引き裂き、磨耗に対してはとても強い素材です。
ところが曲げに対しては弱く、
そのことが柔らかさを感じさせる一因になっているとはいえ
そのままでは弱すぎて都合が悪い場合があります。
同じ革同士でも、貼り合わせることによってある程度の曲げ強さを持たせることができますが、
張りを持たせたい時、あまり曲がってほしくないときなどには
さまざまな素材が芯材としてはさみこまれたり、張り合わされたりして使用されています。
また、厚みを増やしてボリューム感を持たせたい場合などにも芯材は利用されます。
芯材として利用されるものはさまざまで、
革そのもの、再生革、布、紙、樹脂含浸紙、木材、スポンジ、プラスチック、金属・・・
ちょっと考えて思いつく物は、何でも使われている感じです。

このように、目的別にいろいろな材質が利用される芯材ですが、
ここでは重い鞄の底板として使ったり、
パイロットケース型鞄の天板やトランクのフレームとして使う芯材に
何が適しているのか考えてみることにしました。
こういう用途に使われる芯材には、
とにかく曲がらないこと、
それに加えて軽いこと、薄いことなどが要求されます。
また、底鋲の取り付けや横引錠のからくり止めのような局部的な圧縮力にも耐える必要があります。
そうなるとカーボンファイバーコンポジットやハニカム材などが最高の素材と思われますが、
そんな物は、なかなか簡単に入手することはできませんので、
悔しいけれど身近に利用できるものの中から探すことにします。
次の有力候補はFRP
まあ、いいんですけど、自宅で作るとなると臭いがちょっと・・・
靴底の芯としてよく使われる樹脂含浸紙は
いろいろな種類と強度、厚さのものがそろっており、
一見曲げに強そうにも思えるのですが、
クリープ変形と言って、
あまり強くない力でも長い時間かけたままにしておくと
少しずつ変形して行って戻らなくなってしまう性質が強いので、
こういう用途には不向き。
プラスチックダンボールは軽くてよさそうに思えますが、
局部的な圧縮にとても弱いのでだめ。
竹の集成材なんてのもよさそうに思えるのですが、
フローリング用として使われていることは知っているのだが、実際にはどこで買えるんだろう。
そうなると候補として残るのは
ベニヤ板、MDF、アルミ板、硬質発泡塩ビ板などとなりますから、
これらの中からどれが一番優れているか比較することにしましょう。
ベニヤ板は一般的なラワンベニヤや表面がきれいなシナベニヤ、
他にも集成材をベニヤではさんだランバーコアなどがあり、どこでも簡単に入手できます。
むく材と違って吸湿・乾燥での反りや伸び縮みが少ないので気軽に使えます。
MDFとは、Medium Density Fiberboardの略で
木材の繊維を高温高圧の蒸気でほぐしたものを
接着剤を混ぜて圧縮して製作した板材のことです。
木目がないのでどの方向にも均質で、加工しやすい特長があります。
最近ではホームセンターなどでも素材として入手することができます。
アルミ板は少し重いのですが、曲がりにくさは木材の比ではないので、
薄い板を使えば勝ち目があるかもしれません。
硬質発泡塩ビ板もホームセンターの素材コーナーなどで入手することができます。
アクリル板や通常の塩ビ板は重く、ポリエチ板・ポリプロピレン板は柔らかすぎるので、
プラスチック板の中では一番好ましく思えます。
それじゃぁいったいこれらの中から一番強くて軽くて、そのうえ薄いのはどれだってことになるわけですが、
決着をつけるために、まずこれらの素材の性質について代表的な数値を比較したのが下の表です。
| ベニヤ | MDF | アルミ板 | 硬質発泡塩ビ板 | |
| ヤング係数 (kg/cm2) | 67,000 | 25,000 | 720,000 | 10,000 |
| 比重 | 0.5 | 0.55 | 2.7 | 0.78 |
表中のヤング係数とは材料の曲がりにくさを表す数値で、
値が大きいほど曲がりにくい材料であることを示しています。
実際に、これらの板は鞄の底板などとして使用されたときにどれくらい曲がるのでしょうか。
曲がってしまって元に戻らないほど重い物を入れた場合は別として、
壊れない程度に少々たわむときのことを考えます。
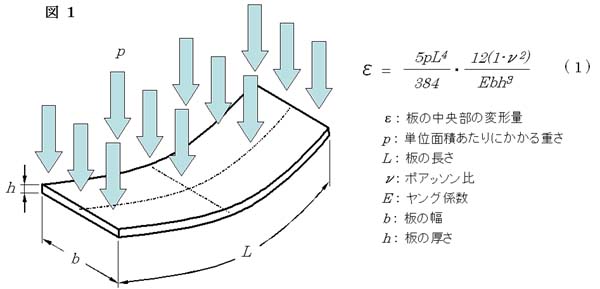
まず、板の両端を持った状態で板面に均等に重さがかかった場合には
下の図1に表したような曲がり方をして、
一番曲がった中央部の変形量ε は式(1)で表した値になります。
どうしてこうなるのかというと・・・・・これはちょっとややこしいので省略。
また、ν はポアッソン比といって、
板を縦方向に引っ張ると縦方向に伸びるだけでなく、横方向に縮むのですが、
この縮みと伸びの比を表しています。
ポアッソン比は材料それぞれに固有の値を持っていますが、だいたいどれも0.3前後です。
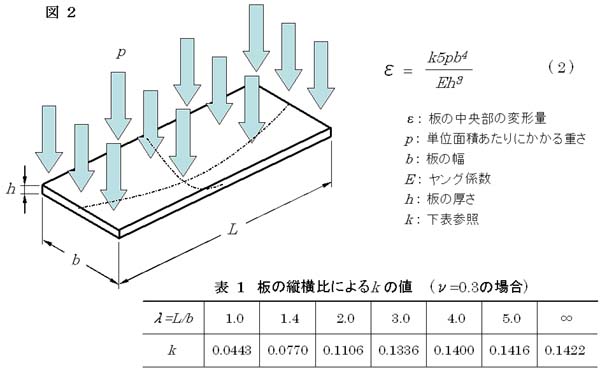
また、板の周囲をすべて押さえた状態では図2のような曲がり方をして、
一番曲がった中央部の変形量ε は式(2)で表した値になります。
どうしてこうなるのかというと・・・・・こっちは更にとてもとてもややこしいので当然省略!
k の値は板の縦と横の長さの比で決まり、図中の表のような値になります。
式(1)、(2)からどちらの場合も板の真ん中の最も曲がったところの変形量は、
板にかかる重さと板の大きさが同じときには、
ヤング係数と、板の厚さの三乗に反比例することがわかります。
ほーっ、厚さを2割5分ほど増やしただけで、板は2倍も曲がりにくくなるのかぁ。
また、そのとき板の重さは比重と板の厚さに比例しますから、
結局次のようなことがわかります。
同じ変形量になるようにしたときの重さと厚みの比較
| ベニヤ | MDF | アルミ板 | 硬質発泡塩ビ板 | |
| 板の重さの比 | 1 | 1.53 | 2.45 | 2.05 |
| 板の厚みの比 | 1 | 1.39 | 0.45 | 1.89 |
同じ重さになるようにしたときの変形量と厚みの比較
| ベニヤ | MDF | アルミ板 | 硬質発泡塩ビ板 | |
| 板の変形量の比 | 1 | 3.57 | 14.7 | 25.4 |
| 板の厚みの比 | 1 | 0.91 | 0.19 | 0.64 |
同じ厚みになるようにしたときの変形量と重さの比較
| ベニヤ | MDF | アルミ板 | 硬質発泡塩ビ板 | |
| 板の変形量の比 | 1 | 2.68 | 0.093 | 6.70 |
| 板の重さの比 | 1 | 1.10 | 5.40 | 1.56 |
なんだ結局ベニヤ板が一番よさそうじゃないか。
ちょっとつまらない気もしますが、
まあ、ちゃんとわかっただけでも良かったかな。